"-Variables- Ley de Ohm-Suma de resistencias-Potencia eléctrica"
"Definición de las variables: "
Intensidad - Diferencia de potencial y Resistencia.
Es el paso de las cargas negativas (electrones) a través de un conductor, es decir un movimiento de cargas. La unidad de medida es el AMPER:
Es la unidad del SI para la intensidad de corriente eléctrica. Podemos conceptualizarla como el paso de un Culombio (6.24 • 10- 18 electrones) en un segundo a través de un conductor. Se representa con la letra "A".
Diferencia de potencial: Hace referencia a la “fuerza que tiene la energía eléctrica” entre los polos positivo y negativo. Esa fuerza es la encargada de mover las cargas eléctricas por un circuito. Es la diferencia de voltaje entre 2 puntos equivalentes al trabajo necesario para mover una carga desde un punto a otro.
Se mide en VOLTIOS:
Se pueden dar dos definiciones diferentes de voltio:
Por un lado, podemos considerar que un voltio es la tensión existente entre dos puntos de un conductor por el que pasa una corriente de un amperio (A) y es disipada una potencia de un vatio (W).
Otra forma alternativa de definirlo: El voltio es equivalente a la diferencia de potencial que existe entre dos puntos de un conductor cuando al transportar entre ellos un culombio (C), se realiza el trabajo de un julio (J).
Es la unidad del SI para el potencial eléctrico, la fuerza electromotriz o el voltaje. Recibe su nombre en honor de Alessandro Volta, quien en 1800 inventó la primera batería química. Es representado simbólicamente por la letra "V".
Resistencia Eléctrica:
Representa la “oposición al paso de la energía eléctrica”.
Se mide en OHMIOS:
Es la unidad del SI para la resistencia eléctrica. Se representa con la letra griega "Ω";
Se define a un ohmio como la resistencia eléctrica que existe entre dos puntos de un conductor, cuando una diferencia de potencial constante de 1 voltio aplicada entre estos dos puntos, produce, en dicho conductor, una corriente de intensidad de 1 amperio (cuando no haya fuerza electromotriz en el conductor).
Genéricamente:
Genéricamente:
Un ohmio es la resistencia eléctrica que presenta una columna de mercurio de 106,3 cm de altura y 1 mm2 de sección transversal, a una temperatura de 0 °C.
"La ley de Ohm"
----La Ley de Ohm relaciona tres magnitudes físicas,como son: la Intensidad, la Diferencia de potencial y la Resistencia, siendo su enunciado el siguiente:La ley de ohm dice que:
"En todo circuito eléctrico la Intensidad de corriente eléctrica que circula por dicho circuito es directamente proporcional a la fuerza electromotriz (fem) aplicada e inversamente proporcional a la Resistencia del circuito."
--Podemos hacer un analogía entre un circuito eléctrico y un circuito hidráulico:
En el símil hidráulico de la siguiente figura, el Voltaje (V) vendría representado por la diferencia de Altura del agua, la Resistencia (R) por el diámetro del tubo, y la Corriente (I) por el Caudal del agua que circula por dicho tubo.
-----------------------------------------------------------------
O sea, que un aumento del Voltaje (mayor Altura de agua) o disminución en la Resistencia (tubo de mayor diámetro), provoca un aumento proporcional en la Corriente eléctrica (mayor Caudal de agua)
La ley de Ohm se aplica a la totalidad de un circuito o a una parte del mismo. Analicemos la parte del circuito que analicemos, siempre se cumplirá.
---De la ecuación de la Ley de Ohm que vimos anteriormente, podemos despejar los valores de Voltaje y de Resistencia.
De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero.
Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso.
Triángulo de la Ley de Ohm
En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda.
Tal vez lo veas más claro en la siguiente animación:
Veamos ahora como aplicar la ley en un circuito sencillo:
Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:
I = V / R = 12v / 10Ω = 1,2 Amperios.

-----Ahora vamos a realizar problemas más complejos:
-------------------------------

-----Ahora vamos a realizar problemas más complejos:
Donde vas a pensar la solución:
1) Si tenemos, 1 Electrón circulando por un circuito eléctrico en un segundo.
A) ¿Podríamos decir que existe una corriente eléctrica?
B) Si así fuere.... ¿Podríamos medir la corriente que genera la circulación de ese circuito?
Leyes de Kirchoff:
1° Ley de Kirchoff: en un nudo eléctrico la suma de las corrientes que ingresan al mismo es igual a la suma de las corrientes que salen de ese nudo.

2° Ley de Kirchoff: “La suma de los voltajes alrededor de una trayectoria o circuito cerrado debe ser cero“,
V4= V1+ V2+V3
En un circuito con varias resistencias en serie.
Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie.
Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación.
En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas.
Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias.
----- Ejercicios:
1) Determinar la Intensidad eléctrica total del circuito.
2) Determinar la Resistencia Total en el circuito.
Es MUY IMPORTANTE tener en cuenta otro factor que completa la definición del circuito y los valores de sus resistencias.
Estoy hablando de la Potencia eléctrica consumida en el circuito, que en el caso de las resistencias se transforma íntegramente en calor.
Si ese calor transformado es muy grande no podrá ser disipado por la resistencia, en este caso ocurre lo que se visualiza en el vídeo:
“La potencia disipada en un circuito eléctrico es directamente proporcional al voltaje y la corriente que circula.”
Por lo tanto:
W (watios) = V (voltios) x I (amperios)
Al hablar de POTENCIA ELÉCTRICA podemos citar :
Donde:
Para fijar conocimientos haremos ejercicios:
Al hablar de POTENCIA ELÉCTRICA podemos citar :
"La Ley de Joule"
"Toda potencia que se desarrolla ante el paso de una corriente por una Resistencia , se transforma en calor."
........ depende de las siguiente variables:
P=I2 x R esto es en watt, esto mismo expresado en calorías: Q = I 2 x R x 0,24 cal/seg.
P=I2 x R esto es en watt, esto mismo expresado en calorías: Q = I 2 x R x 0,24 cal/seg.
Donde:
Q= calor
I 2 x R= potencia eléctrica
0,24 cal/seg = equivalente entre potencias eléctricas.
1) a-¿Por qué se destruye un resistor?
Rta. ….. Resuelto matemáticamente:…..
Suponemos:
R1= 1 Ω (resistencia quemada) y,
R1= Disipa 1W/seg.
b- ¿Qué pasa si en los terminales aplico una f.e.m. de 12 Voltios?
c- ¿Con ésta Intensidad de corriente de 12 A ¿Cuál será la Potencia que circula por la misma?
--------------------------------------------
2) Si compramos 1 R cuya potencia es de 500 W....
Sabiendo que esta R es de 24 Ω sometida a una f.e.m. de 220 V y,
si la divido por la mitad en 2 Resistencias.....
a- ¿Cuánta potencia puedo obtener?
b- ¿Es conveniente hacer esto? Por qué?
c-¿Por qué la potencia eléctrica es transportada por alta tensión? (por ej: desde una central de generación hasta nuestros hogares).
Rta:
La energía eléctrica se transporta en alta tensión para disminuir las pérdidas asociadas al efecto Joule (calentamiento de los conductores), que es proporcional a la intensidad que circula por los cables. Para la misma potencia, mayor tensión significa menor intensidad (P=I·V), por lo que al elevar la tensión se disminuye la intensidad y por tanto las pérdidas.
-----------------------------------------------
Potencia Mecánica- Torque:



------------------------------------------------
Capacidad Eléctrica
---------------------------------------------------------------------------
Magnetismo:
Es la fuerza de atracción por cuerpo metálicos.
Clasificación de los materiales magnéticos:
| Tipo de material | Características |
|---|---|
| No magnético | No afecta el paso de las líneas de campo magnético. Ejemplo: el vacío. |
| Diamagnético | Material débilmente magnético. Si se sitúa una barra magnética cerca de él, esta lo repele. Ejemplo: bismuto (Bi), plata (Ag), plomo (Pb), agua. |
| Paramagnético | Presenta un magnetismo significativo. Atraído por la barra magnética. Ejemplo: aire, aluminio (Al), paladio (Pd), magneto molecular. |
| Ferromagnético | Magnético por excelencia o fuertemente magnético. Atraído por la barra magnética. Paramagnético por encima de la temperatura de Curie (La temperatura de Curie del hierro metálico es aproximadamente unos 770 °C). Ejemplo: hierro (Fe), cobalto (Co), níquel (Ni), acero suave. |
| Antiferromagnético | No magnético aun bajo acción de un campo magnético inducido. Ejemplo: óxido de manganeso (MnO2). |
| Ferrimagnético | Menor grado magnético que los materiales ferromagnéticos. Ejemplo: ferrita de hierro. |
| Superparamagnético | Materiales ferromagnéticos suspendidos en una matriz dieléctrica. Ejemplo: materiales utilizados en cintas de audio y video. |
| Ferritas | Ferromagnético de baja conductividad eléctrica. Ejemplo: utilizado como núcleo inductores para aplicaciones de corriente alterna. |
Temperatura de Curie:
Curie determinó que a los 750°C pierde el hierro todas las propiedades magnéticas. Es decir, que a partir de 750°C el material se vuelve Amagnético.
Masa magnética:
Definición de masa magnética:
Cantidad de magnetismo de un imán, o sea, la intensidad de su fuerza atractiva.
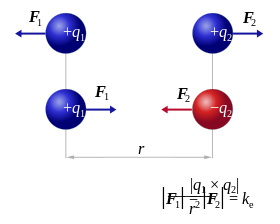
La ley de Coulomb puede expresarse como:
|
F= M1 x M2
d2
d2
Ley de Coulomb expresando los signos de cargas de diferente signo, y de cargas del mismo signo.
Intensidad de Campo magnético:
Se denomina con la letra "H" y está dada por la fuerza que actúa sobre una unidad de masa magnética (UMM), en un punto dado. De modo que si se tiene en un punto cualquiera de un campo magnético, una masa magnética unitaria, que sobre ella actúa la fuerza de una Dina, diremos que, en tal punto la Intensidad de campo magnético es de 1 Gauss, y la fuerza está dada por:
F= H x M
Flujo Magnético:
El flujo magnético (representado por la letra griega fi Φ), es una medida de la cantidad de magnetismo, y se calcula a partir del campo magnético. La unidad de flujo magnético en el Sistema Internacional de Unidades es el weber y se designa por Wb (motivo por el cual se conocen como weberímetros los aparatos empleados para medir el flujo magnético). En el sistema cegesimal se utiliza el maxwell (1 weber =108 maxwells).
El flujo magnético (representado por la letra griega fi Φ), es una medida de la cantidad de magnetismo, y se calcula a partir del campo magnético. La unidad de flujo magnético en el Sistema Internacional de Unidades es el weber y se designa por Wb (motivo por el cual se conocen como weberímetros los aparatos empleados para medir el flujo magnético). En el sistema cegesimal se utiliza el maxwell (1 weber =108 maxwells).

Flujo magnético por una espira
El flujo magnético (representado por la letra griega fi Φ), es una medida de la cantidad de magnetismo, y se calcula a partir del campo magnético, la superficie sobre la cual actúa y el ángulo de incidencia formado entre las líneas de campo magnético y los diferentes elementos de dicha superficie.
Es decir, se define al flujo magnético Φ ,como la cantidad de líneas de campo magnético que atraviesan una determinada superficie S en el espacio.
Donde: Φ =flujo magnético.
B= inducción magnética.
H= intensidad de campo magnético
S= sección o superficie.
Φ= H x S =H.S.cos Θ
El Flujo Magn. se mide en maxwells y,
maxwells= Gauss x cm2
Influencia de la materia contenida en el Campo magnético:
El flujo que circula entre 2 polos es afectado por el material que se encuentra entre dichos polos, si el material es ferromagnético, el flujo será afectado por la permeabilidad magnética.
flujo= intensidad de campo X permeabilidad magnética X superficie
"Electromagnetismo:"
 La ley de Biot-Savart indica el campo magnético creado por corrientes estacionarias. En el caso de corrientes que circulan por circuitos cerrados, la contribución de un elemento infinitesimal de longitud dl del circuito recorrido por una corriente I crea una contribución elemental de campo magnético, dB, en el punto situado en la posición que apunta el vector Ur a una distancia R respecto de dl , quien apunta en dirección a la corriente I:
La ley de Biot-Savart indica el campo magnético creado por corrientes estacionarias. En el caso de corrientes que circulan por circuitos cerrados, la contribución de un elemento infinitesimal de longitud dl del circuito recorrido por una corriente I crea una contribución elemental de campo magnético, dB, en el punto situado en la posición que apunta el vector Ur a una distancia R respecto de dl , quien apunta en dirección a la corriente I:

 donde J es la densidad de corriente en el elemento de volumen dv y R es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
donde J es la densidad de corriente en el elemento de volumen dv y R es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
En ambos casos, el campo final resulta de aplicar el proncipio de superposición a través de la expresión
 en la que la integral se extiende a todo el recinto que contiene las fuentes del campo.
en la que la integral se extiende a todo el recinto que contiene las fuentes del campo.
La ley de Biot-Savart es fundamental en magnetostática tanto como la ley de Coulomb lo es en electrostática.
Definimos también, elemento de corriente a la intensidad que circula por un elemento de longitud dl.
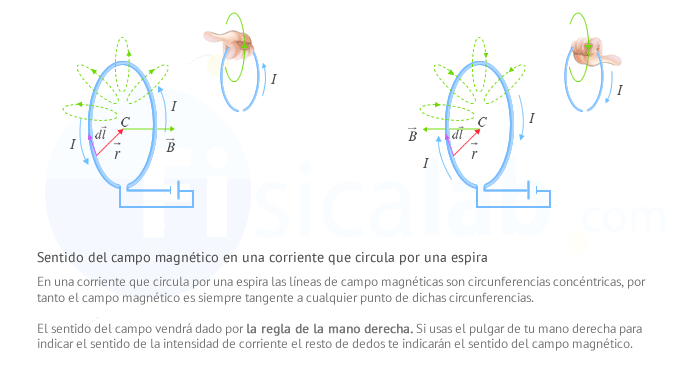
Campo magnético creado por una corriente eléctrica que circula por una espira
"Ley de Hopkinson":

En el caso de un solenoide largo y con cierto número de vueltas, la expresión se puede simplificar. En este caso se expresa por la siguiente ecuación.

PÉRDIDAS POR HISTÉRISIS:
jueves, 18 de junio de 2009
Ley de Biot-Savart
 La ley de Biot-Savart indica el campo magnético creado por corrientes estacionarias. En el caso de corrientes que circulan por circuitos cerrados, la contribución de un elemento infinitesimal de longitud dl del circuito recorrido por una corriente I crea una contribución elemental de campo magnético, dB, en el punto situado en la posición que apunta el vector Ur a una distancia R respecto de dl , quien apunta en dirección a la corriente I:
La ley de Biot-Savart indica el campo magnético creado por corrientes estacionarias. En el caso de corrientes que circulan por circuitos cerrados, la contribución de un elemento infinitesimal de longitud dl del circuito recorrido por una corriente I crea una contribución elemental de campo magnético, dB, en el punto situado en la posición que apunta el vector Ur a una distancia R respecto de dl , quien apunta en dirección a la corriente I:
donde μ0 es la permeabilidad magnética del vacío, y Ur es un vector unitario.
En el caso de corrientes distribuidas en volúmenes, la contribución de cada elemento de volumen de la distribución, viene dado por
En el caso de corrientes distribuidas en volúmenes, la contribución de cada elemento de volumen de la distribución, viene dado por
 donde J es la densidad de corriente en el elemento de volumen dv y R es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
donde J es la densidad de corriente en el elemento de volumen dv y R es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.En ambos casos, el campo final resulta de aplicar el proncipio de superposición a través de la expresión

La ley de Biot-Savart es fundamental en magnetostática tanto como la ley de Coulomb lo es en electrostática.
Definimos también, elemento de corriente a la intensidad que circula por un elemento de longitud dl.
El valor del campo magnético en el centro de una espira circular creado por una corriente eléctrica se obtiene por medio de la siguiente expresión:
donde:
- B es el valor del campo magnético en el centro de la espira C. Su unidad en el S.I. es el Tesla (T).
- μ0 es la permeabilidad magnética del vacío. En el S.I. se mide en m·kg/C2.
- I es la intensidad de corriente que circula por la espira. Su unidad en el S.I. es el Amperio (A).
- R es el radio de la espira. Su unidad en el S.I. es el metro (m).
Las líneas de campo creadas por este tipo de corriente son circunferencias concéntricas en cada punto del conductor, de tal forma que en el centro de la espira el campo magnético es perpendicular a la espira y el sentido se obtiene aplicando la regla de la mano derecha. Recuerda que como hemos dicho antes, la regla de la mano derecha determina que si usamos el pulgar de dicha mano para indicar el sentido de la intensidad de corriente, el resto de dedos nos indicarán el sentido del campo magnético.

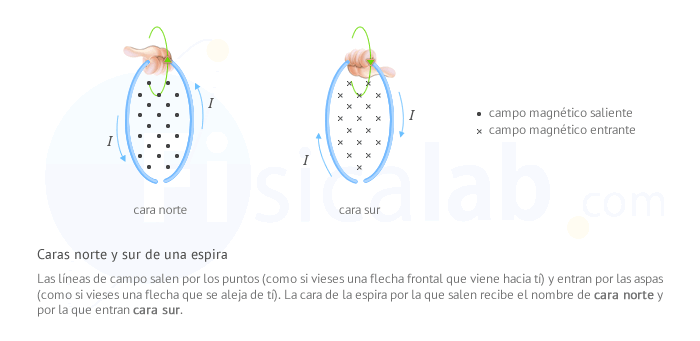
Independientemente de cual sea el sentido de la intensidad de la corriente eléctrica, las líneas de campo saldrán por una cara de la espira y entrarán por otra. La cara por la que salen recibe el nombre de cara norte y por la que entran cara sur, al igual que ocurre con un imán.

Comprobación
Aplicando la ley de Biot y Savart, la dirección y sentido del campo magnético en el centro de la espira vendrá dado por el producto vectorial entre dl→ y r→ :
Fuerza magnetomotriz
La fuerza magnetomotriz (FMM, representada con el símbolo F) es aquella capaz de producir un flujo magnético entre dos puntos de un circuito magnético. Es una de las variables usadas para describir un campo magnético.
La fuerza magnetomotriz se puede entender de manera análoga al voltaje eléctrico de la ley de Ohm. Esto está expresado en la ley de Hopkinson.
El potencial magnético o fuerza magnetomotriz, es la fuente que produce el flujo magnético en un circuito magnético.
La Fuerza magnetomotriz de un circuito magnético se puede expresar en términos del flujo magnético Φ y la reluctancia magnética Rm
Esta ecuación se puede entender como una analogía a la ley de Ohm ( V = R I ). El flujo magnético es directamente proporcional a la Fuerza magnetomotriz que lo origina e inversamente proporcional a la reluctancia del circuito magnético que depende de la longitud del circuito, el área transversal del circuito y la permeabilidad magnética del material del que está hecho. Las variables magnéticas se comportan como sus análogas eléctricas en la ley de Ohm.
El flujo magnético sigue las líneas de flujo por donde encuentra menor reluctancia. Por esto las líneas de flujo están dentro del cuerpo de alta permeabilidad, puesto que esto ofrece mucha menor reluctancia que el aire. Sin embargo el cuerpo de alta permeabilidad aún posee cierta reluctancia que es el equivalente a la resistencia en esta analogía de Hopkinson. El flujo magnético sería el equivalente a la corriente eléctrica.
Usualmente en los circuitos eléctricos simples (como en la Figura) la fuerza magnetomotriz se genera empleando un solenoide. Esto es un alambre aislado enrollado en forma de hélice.

En el caso de un solenoide largo y con cierto número de vueltas, la expresión se puede simplificar. En este caso se expresa por la siguiente ecuación.
donde:
La unidad de medida de la FMM es el amperio-vuelta que se representa por Av.
La relación existente entre la fuerza magnetomotriz y el flujo magnético que esta genera se denomina reluctancia y se determina por la expresión:
donde:
- Φ: Flujo magnético en weber.
- : Reluctancia del circuito en amperio vuelta dividido weber.

Pérdidas de circuitos magnéticos:
PÉRDIDAS POR HISTÉRISIS:
Las pérdidas por histéresis representan una pérdida de energía que se manifiesta en forma de calor en los núcleos magnéticos y esto hace que se reduzca el rendimiento del dispositivo. Con el fin de reducir al máximo estas pérdidas, los núcleos se construyen de materiales magnéticos de características especiales, como por ejemplo acero al silicio. Por ejemplo, para la fabricación de imanes permanentes se eligen materiales que posean un campo coercitivo lo más grande posible.

PERDIDAS POR CORRIENTES PARÁSITAS O DE FOUCAULT:
Las corrientes parásitas son corrientes que
circulan en el interior de conductores como
consecuencia de campos magnéticos
variables con el tiempo. Estas corrientes circulares
crean electroimanes con campos magnéticos
que se oponen al efecto del campo magnético
aplicado. Cuanto mas fuerte sea el campo
magnético aplicado o mayor la conductividad
del conductor o mayor la velocidad relativa
de movimiento, mayores serán las corrientes
parásitas y los campos opositores generados.
-Si una corriente atraviesa a un conductor se va a originar una serie de corrientes a las que llamaremos corrientes parásitas o de Foucault que van a oponerse a la variación de flujo magnético.
Estas le restan eficacia a eléctrica a dispositivos como transformadores y bobinas.
-Se producen sobre conductores que estén sometidos a flujos magnéticos variables.
-Provocan una perdida de potencia de la máquina.
-Aumenta la temperatura del núcleo magnético.
-Para minimizar su efecto el núcleo magnético se lamina.
Ley de Lenz: y ley Faraday


--------------------------
Reactancia
En electrónica y electrotecnia se denomina reactancia a la oposición ofrecida al paso de la corriente alterna por inductores (bobinas) y condensadores, se mide en ohmios y su símbolo es Ω. Junto a la resistencia eléctrica determinan la impedancia total de un componente o circuito, de tal forma que la reactancia (X) es la parte imaginaria de la impedancia (Z) y la resistencia (R) es la parte real, según la igualdad:
Tipos de reactancias
Cuando circula corriente alterna por alguno de los dos elementos que poseen reactancia, la energía es alternativamente almacenada y liberada en forma de campo magnético, en el caso de las bobinas, o de campo eléctrico, en el caso de los condensadores. Esto produce un adelanto o atraso entre la onda de corriente y la onda de tensión. Este desfase hace disminuir la potencia entregada a una carga resistiva conectada tras la reactancia sin consumir energía.
Si se realiza una representación vectorial de la reactancia inductiva y de la capacitiva, estos vectores se deberán dibujar en sentido opuesto y sobre el eje imaginario, ya que las impedancias se calculan como y respectivamente.
No obstante, las bobinas y condensadores reales presentan una resistencia asociada, que en el caso de las bobinas se considera en serie con el elemento, y en el caso de los condensadores en paralelo. En esos casos, como ya se indicó arriba, la impedancia (Z) total es la suma vectorial de la resistencia (R) y la reactancia (X).
En fórmulas:
Donde:
- "j" es la unidad imaginaria
- es la reactancia en ohmios.
ω es la velocidad angular a la cual está sometido el elemento, L y C son los valores de inductancia y capacidad respectivamente.
Dependiendo del valor de la energía y la reactancia se dice que el circuito presenta:
- Si , reactancia inductiva .
- Si , no hay reactancia y la impedancia es puramente resistiva .
- Si , reactancia capacitiva .
Reactancia capacitiva:
La reactancia capacitiva se representa por y su valor viene dado por la fórmula:
en la que:
Reactancia inductiva
La reactancia inductiva es representada por y su valor viene dado por:
en la que:
= Reactancia inductiva en ohmios.
= Inductancia en henrios.
= Frecuencia en hercios.
= Velocidad angular.
= Inductancia en henrios.
= Frecuencia en hercios.
= Velocidad angular.
-------------------------
"Motores sincrónicos y asincrónicos": (ejercicios)
"Motor trifásico: Partes -Funcionamiento "
"Motor de corriente continua"
Potencias: (ejercicios)
"Generación de corriente alterna:"













 : Reluctancia del circuito en amperio vuelta dividido weber.
: Reluctancia del circuito en amperio vuelta dividido weber.


















como le paso la cabeza a Amp por ese tubo si es mas delgado?
ResponderEliminaro es que paso antes que Omh se diera cuenta y apretara la soga?
Eliminar